Analysis of Sand Water Ratio and Drying Unit Weight Using Flat TDR System

Flat TDR 시스템을 이용한 모래의 함수비와 건조단위중량 분석

Abstract

In this study was conducted to measure the water content and dry unit weight of the ground using TDR (Time Domain Reflectometry) in order to supplement the problems of the conventional compaction management method. The Flat TDR system is a device that does not cause ground disturbance, and in order to verify the measured values, the dry density and water content were measured for samples of the ground subject at 7 sites other than Jumunjin Standard Temple. The water content section was divided into 6 sections of 3, 6, 9, 12, 15, and 18%, and the experimental results were confirmed according to the unified classification method. As a result of the indoor experiment, the water content showed an error of about 0.7% for the SP sample and about 1.3% for the SM sample. In addition, the dry unit weight confirmed an error of about 7% for the SP sample and about 5% for the SM sample. It was confirmed that stable values were derived in sandy or silty sandy ground except for clay or gravel. Through the experimental results, it was confirmed that the measured values of the flat TDR system derive similar values to the existing traditional compaction management method, and it was determined that the flat TDR equipment was suitable for construction sites that require quick constructability and economic feasibility.

본 연구에서는 기존의 전통적인 다짐관리방법의 문제점을 보완하고자 TDR(Time Domain Reflectometry)을 이용하여 지반의 함수비와 건조단위중량을 측정하는 연구를 수행하였다. Flat TDR 시스템은 지반의 교란을 일으키기 않는 장비로써 측정값을 검증하기 위하여 주문진표준사 외 7개소의 현장대상 지반의 시료에 대하여 건조밀도와 함수비를 측정하였다. 함수비구간은 3, 6, 9, 12, 15, 18%의 6개 구간으로 나누어 측정을 하였으며 실험결과는 통일분류법에 따라 확인하였다. 실내실험 결과, 함수비는 SP시료의 경우 약 0.7%, SM시료의 경우 약 1.3%의 오차를 보였다. 또한 건조단위중량은 SP시료의 경우 약 7%, SM시료의 경우 약 5%의 오차를 확인하였다. 이는 점토나 자갈을 제외한 모래 또는 실트질 모래 지반에서는 안정적인 값을 도출함을 확인할 수 있었다. 실험 결과를 통하여 Flat TDR 시스템의 측정값이 기존의 전통적인 다짐관리방법과 유사한 값을 도출하는 것을 확인할 수 있었고 이는 빠른 시공성과 경제성을 필요로하는 건설현장에서 Flat TDR 장비가 적합하다는 것을 판단할 수 있었다.

서론

연구배경 및 목적

다짐은 저수지 제방 및 댐, 고속도로 등 구조물의 기초의 안정성을 증대시키기 위해 흙속의 공기를 제거하여 흙의 강도 특성을 증가시키는 것으로 성토사면의 안정성을 확보하고 구조물의 불필요한 침하량을 감소시키는 등 흙 구조물 공사의 필수 공정이다. 국내 현장에서는 표준시방서의 다짐기준을 만족시키기 위해서 주로 모래치환법과 평판재하시험을 이용하여 다짐관리를 한다. 위 시험방법은 시험을 수행하는 사람에 따른 오차를 정량화하기 어렵고 때로는 현장여건의 한계로 시험이 불가능한 경우가 발생하기도 한다. 이러한 문제점을 보완하기 위해서 신속하고 경제적이며 지반교란을 최소화 할 수 있는 비파괴 시험법 및 현장 관입시험의 수요가 점차 증가하고 있다.

이와 관련하여, 대표적으로 시간영역반사법(Time Domain Reflectometry, 이하 TDR)을 이용한 연구가 진행되고 있다. Topp et al.(1980)은 토양 내에 포함된 물의 양에 의해서 토양의 유전율이 강하게 영향받는다는 것을 입증하였며, TDR 신호를 금속봉을 통해 원위치지반에 전송하여 흙의 체적 함수비를 측정하는 방법을 연구하였다. 미국 Purdue 대학의 Drnevich 교수 연구진에 의해서 현장지반의 건조단위중량과 함수비를 측정하는 ASTM D6780-05(2005) 방법이 개발되었고, Yu and Yu(2006)는 기존에 제안되었던 체적함수비, 중량함수비 및 건조단위중 량의 식을 다층토에 대하여 적용시키는 연구를 수행 하였다. Jung et al.(2013)은 새로운 중량함수비 및 건조단위중량 의 식을 제안하였고, 높은 함수비의 흙이나 세립분이 많이 함유된 흙에서는 기존의 Yu and Drnevich(2004)가 제안한 중 량함수비및건조단위중량식이 정확한 값을 도출하기 어렵다고 판단하였다.

Thring et al.(2014)은 겉보기 유전율 측정값으로 도출해낸 체적함수비와 건조단위중량으로부터 중량 함수비를 비교적 간단히 추정할 수 있는 세 가지 방법을 제안하였다. Song et al.(2015)은 주문진 표준사및 화강풍화토를 대상으로 실험하여 검증을 하였으며, Jung et al.(2013)에 의해 제안된 함수비 예측을 위한 보정방정식의 문제점을 보완하여 새로운 보정방정식을 제안하였다.

기존의 Purdue TDR 시스템은 봉형 프로브를 사용하기 때문에 몇 가지 문제점이 발생할 수 있다. 봉형 프로브는 망치로 타격하여 프로브를 지반에 관입을 시켜야 하는 소정의 작업이 필요하기 때문에, 주변 지반을 교란시킬 수 있고, 단단한 지반에 관입에는 어려움이 따르는 문제점이 있다.

이러한 문제점을 해결하기 위해 Song(2016)은 Flat 프로브를 개발하여 지반 표면에서 측정할 수 있도록하여 기존의 봉 형 프로브의 문제점을 개선하였다. 개발한 Flat 프로브의 측정값을 검증하기 위해 네 가지 시료를 사용하였고, 각각의 시료의 함수비 및 다짐도를 변화시키며 실내실험을 수행하였다. 그 결과 함수비의 경우 오차범위 약 0.5%, 건조 단위중량의 경우 오차범위 약 2%의 오차를 보였다. 또한 Song et al.(2016)은 함수비와 건조단위중량의 측정과 동시에 지반의 강성을 측정하기 위해 개발한 Flat 프로브에 탄성파 측정 장치인 Piezoelectric stack을 결합하여 하였다. 시료에 그라우팅용 마이크로 시멘트를 혼합하여 기중양생을 진행하여 시간의 경과에 따른 탄성계수를 측정하였고, 이를 통해 탄성파 측정 시스템의 현장 적용성을 검토하였다. 그 결과 압축파 및 전단파의 도달시간이 양생기간이 늘어남에 따라 단축됨 확인하였고, 탄성계수를 전파속도를 바탕으로 산정할 수 있다고 확인하였다.

본 연구에서는 Flat TDR 시스템의 함수비와 건조단위중량 측정값에 대한 정밀도와 신뢰성 확보를 위해 주문진표준사를 포함한 7개소 대상현장지반의 시료를 사용하여 실내실험을 수행하였고, Flat TDR 시스템의 측정값과 실측값을 비교하여 정밀도를 확인하였다. 또한 각 시료를 통일분류법에 따라 분석하여 SP, SM 시료로 나누어 비교 분석하여 지반의 특성에 따른 결과를 확인하고자 하였다.

TDR 적용 이론

TDR의 측정 기본 원리

TDR 시스템은 신호 발생기에서 발생한 전자기파가 흙 속에서 이동하고, 그 전도 특성을 이용하는 시스템이다. 이러한 특성을 이용해 흙 속에 관입된 프로브의 전자기파의 반향 시간을 측정하고 반향 특성을 이용하여 흙의 유전상수 및 전기 전도도를 측정한다. 이와 같은 원리를 통해 흙의 유전상수 및 전기전도도를 이용하여 함수비 및 밀도를 평가한다.

함수비와 건조단위중량 측정

Fig. 1a는 Purdue TDR 시스템을 보여주며, 흙의 유전상수(K_a) 및 전기전도도(EC_b)는 Fig. 1b와 같은 TDR 신호 전파에서 얻을 수 있다. Fig. 1a에서 흙 속에 관입된 프로브의 길이를 (L_p)라 하고, Fig. 1b에서 첫 번째 반사 지점과 두 번째 반사 지점 사이의 거리를 겉보기 길이(L_a)라고 하여 흙의 유전상수(K_a)는 식 (1)과 같이 표현할 수 있다.

Fig. 1. Components of the TDR system and typical TDR waveform (Yu and Drnevich, 2004).

\(K_{a}=\left(\frac{L_{a}}{L_{P}}\right)^{2}\)       (1)

또한 전기전도도(EC_b)는 식 (2)와 같이 표현할 수 있다.

\(E C_{b}=\frac{1}{C}\left(\frac{V_{s}}{V_{f}}-1\right)\)       (2)

여기서, V_s는 스텝 펄스의 두 배 크기의 전압이며, V_f는 장주기전압레벨이다. 그리고 C는 프로브의 구조에 관련된 상수이며, 식 (3)과 같이 정의할 수 있다(Giese and Tiemann, 1975; Yu and Drnevich, 2004). 여기서 R_e는 TDR 신호 생성기 의 내부저항(50Ω)이다.

\(C=\frac{2 \pi R_{s} L_{p}}{\ln \left(\frac{d_{o}}{d_{i}}\right)}\)       (3)

Siddiqui et al.(2000)은 기존의 함수비 보정식들이 체적함수비로 표현되고, 밀도효과를 포함하고 있어 복잡하고 현장에서 바로 적용하기 어렵다고 하여 중량함수비로 이루어진 식 (4)를 제안하였고, 이는 다양한 흙에 대하여 만족스러운 결과를 보여주었다(Sallam et al., 2004).

\(\sqrt{K_{a}} \frac{\rho_{w}}{\rho_{d}}=a+b w\)       (4)

여기서, \(\rho_\omega\)는 물의 단위중량, \(\rho_d\)는 흙의 건조단위중량, \(\omega\)는 중량함수비, 그리고 a와 b는 흙의 특성상숫값 이다.

또한 Yu and Drnevich(2004)는 기존의 전기전도도에 관한 식이 단위중량에 대한 고려가 없으며 체적함수비로 표현되어 있어 지반공학적으로 응용하는데 부족하고, 흙의 총 전기전도도의 지배 요인은 간극 유체의 전기전도도이기 때문에 간극 유체의 양이 흙의 총 전기전도도를 지배한다고 보고 식 (5)를 제안하였다.

\(\sqrt{E C_{b}} \frac{\rho_{w}}{\rho_{d}}=c+d w\)       (5)

여기서, c와 d는 흙의 특성상수 값이며, 식 (4)와 식 (5)를 이용하여 흙의 특성상숫값을 산정하고, 측정된 유전상수와 총 전기전도도를 이용하여 식 (6), (7)과 같이 현장지반의 건조단위중량과 함수비를 계산할 수 있다(Yu and Drnevich, 2004).

\(\rho_{d}=\frac{d \sqrt{K_{a}}-b \sqrt{E C_{b}}}{a d-c b} \rho_{w}\)       (6)

\(w=\frac{c \sqrt{K_{a}}-b \sqrt{E C_{b}}}{b \sqrt{E C_{b}}-d \sqrt{K_{a}}}\)       (7)

Flat TDR 시스템 구성

TDR 측정 장비

본 연구에서는 TDR 프로브를 통해 전파된 펄스가 지반에 접촉된 프로브를 따라 다시 반사되어 오는 것을 계측하기 위해 Fig. 2a와 같이 CAMPBELL SCIENTIFIC, INC.(USA)에서 제작한 TDR 측정 시스템을 사용하였다. TDR 측정 시스템을 살펴보면 Fig. 2b와 같이 TDR 시스템에 전원을 공급하기 위한 12 V 배터리, 탄성계수 예측을 위한 PC 오실로스코프, TDR 프로브에 신호를 보내 반사된 신호를 측정할 수 있는 TDR100으로 구성되어 있다.

Fig. 2. TDR100 device (CAMPBELL SCIENTIFIC, INC.) and TDR system device.

Flat 프로브

본 연구에서 사용한 Flat 프로브의 크기는 30.5*30.5 cm의 폴리머 재질의 판에 폭 2.5 cm의 구리 띠가 부착되어있다. Knight et al.(1997), Ferré et al.(1998)이 제안한 유한요소해석을 통하여 프로브의 크기를 결정하였고,

구리 띠 사이의 간격은 5 cm로 총 세 개가 부착되어 있다. 기존 봉형 프로브와 달리 지반 표면에 접촉시켜 측정하는데 이 때 매질 차이에 의한 전파 간섭 문제를 해결하기 위해서 폴리머 재질이 사용되었다(Fig. 3).

Fig. 3. Flat probe.

실내실험

실내 실험 시료

본 절에서는 각 시료에 따른 TDR 신호와 측정값에 대한 정밀도를 분석하기 위해 총 주문진표준사를 포함한 7개소의 대상현장지반의 시료를 사용하였으며, 사용한 시료는 주문진 표준사와 강진 현장 시료, 울주 현장의 시료, 섬진강에서 채취한 시료, 원주 현장 시료, 경주 현장 시료, 전남 옥과 현장시료를 사용하여 실험을 진행하였다. Fig. 4는 실험에 사용된 시료들의 입도분포 곡선이다. Table 1은 실험에 사용된 시료의 물성치이다.

Fig. 4. Particle size distribution curve.

Table 1. Fixed physical property value

Flat TDR 실험

본 절에서는 Flat TDR 시스템의 측정값에 대한 정밀도를 확인하기 위해 여섯 가지의 시료를 이용하여 함수비와 단위 중량의 변화에 따른 TDR 파형을 측정하여, 각 시료에 따른 전기전도도와 유전상수를 측정하였다. 함수비를 3~15%의 범위에서 3%씩 변화시켰으며 증류수를 사용하여 함수비를 조성하였다. 다짐은 A 다짐봉으로 3층 40회 다짐을 실시하였고 균일한 다짐을 위해 Fig. 5a와 같은 철판과 몰드(33*33*10 cm)를 제작하여 시료 위에 올려놓고 다짐봉으로 타격하였다. Flat TDR 실험은 다음과 같은 절차로 수행되었다.

Fig. 5. Flat TDR test process.

(1) 제작한 몰드에 적당한 양의 시료를 넣고 철판을 올린 뒤 A 다짐봉으로 3층 40회 다짐을 한다.

(2) 다짐 완료 후 몰드의 칼라를 제거한 뒤 트리머를 이용하여 시료를 제거한다. 시료의 성형이 완료되면 몰드와 함께 시료의 무게를 측정한다.

(3) 다져진 시료 위에 Flat 프로브를 올려놓고 TDR신호를 측정한다. 신호의 측정은 3회 실시한다.

(4) TDR 신호 측정이 끝난 후 몰드의 중앙에서 시료를 채취하여 실측 함수비를 측정한다.

(5) 함수비 측정까지 끝난 후 다시 함수비를 조성하여 3%씩 증가시키며 15%의 함수비까지 (1)~(4)를 반복하여 실시한다.

실내 실험 결과

시료별 특성 상숫값 결정

7가지 시료를 통해 함수비와 단위중량의 변화에 따라 Flat TDR 시스템의 신호를 2장에서 기술한 이론을 바탕으로 분석하였고, 각 시료의 유전상수 및 전기전도도를 측정하여 보정 계수를 산출하였다. 2.2에서 제시한 식 (6), (7)을 사용하여 함 수비와 유전상수 및 전기 전도도와의 관계에 대해 선형회귀분석을 수행하였고, 각 시료의 특성 상숫값은 Table 2와 같다.

Table 2. Fixed physical property value

Flat TDR 시스템의 검증실험결과

Fig. 6은 Flat TDR 시스템을 이용하여 유전상수와 전기전도도, 각 시료의 특성상숫값을 도출하여 측정된 함수비와 건조단위 중량이다. 실측 함수비와 건조 단위중량을 측정하고, Flat TDR 시스템으로 측정한 값과 비교하여 정밀도를 분석 하였다.

Fig. 6. Water content result graph of inddor experiment and TDR equipment.

함수비

본 연구에서 Flat TDR 시스템을 이용하여 7가지 시료의 함수비를 측정하였으며, 각 시료의 측정된 함수비와 실측 함수 비는 통일분류법에 따라 분석하였다.

Fig. 6은 주문진 표준사를 포함한 7개소 대상지반에 대한 함수비를 측정하여 실내 다짐시험과 비교하여 분석한 것이고 Table 3은 결괏값들을 나열한 것이다. 그 결과, SP시료에서는 99.28%, SM시료에서는 98.7%이상의 신뢰도를 확인할 수 있었다.

Table 3. Comparison of water content between indoor compaction test and flat TDR (Real measured/TDR test measured)

건조단위중량

본 연구에서 Flat TDR 시스템을 이용하여 7가지 시료의 건조단위 중량을 측정하였으며, 각 시료의 측정된 건조단위 중량과 실측 건조단위중량은 주문진 표준사의 실험값과 비교하였다.

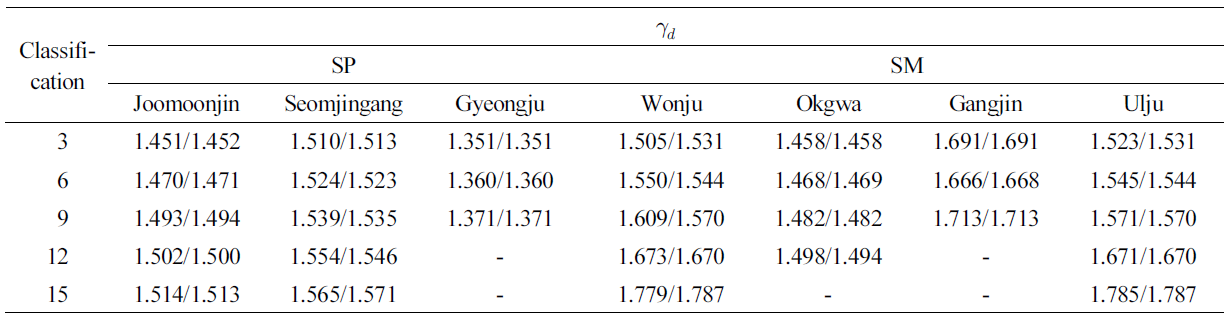
Fig. 7은 주문진 표준사를 포함한 7개소 대상지반에 대한 건조단위중량을 측정하여 실내 다짐시험과 비교하여 분석한 것이고 Table 4는 결괏값들을 나열한 것이다. 그 결과, SP시료에서는 92.97%, SM시료에서는 94.91% 이상의 신뢰도를 확인할 수 있었다.

Table 4. Comparison of dry unit weight between indoor compaction test and flat TDR (Real measured/TDR test measured)

Fig. 7. Dry unit weight result graph of indoor experiment and TDR equipment.

결론

본 연구에서는 전통적인 다짐관리방법의 문제점을 보완하고 신속한 다짐 관리를 위해 Flat Type의 프로브를 제작하였다. Flat 프로브는 지반 표면에서 측정하기 때문에 기존의 다짐관리방법의 문제점인 지반 교란을 발생시키지 않으며 추가적인 소정의 작업이 없어 보다 신속하고 간편하다는 장점이 있다. 이러한 Flat TDR 시스템 측정값의 신뢰성과 정밀도를 검증하기 위해 주문진 표준사를 포함한 7개소의 대상현장지반의 시료를 사용하여 Flat TDR 시스템으로 함수비와 건조단 위중량을 측정하였다. 또한 Flat TDR시스템으로 도출된 함수비와 건조단위중량 측정값과 비교분석을 위한 실측값 도출을 위하여 실내실험을 수행하였고, 각각의 측정값을 비교분석하였다. 일련의 연구를 통하여 다음과 같은 결론을 얻었다.

(1) Flat TDR 시스템으로 각각 시료의 특성상수와 유전상수, 전기전도도의 값을 도출하였고, 도출된 값을 바탕으로 하여 함수비와 건조단위중량을 산정하였다. 실측값과 비교하였을 때, 측정된 함수비는 평균적으로 약 1%의 오차를 보였으며, 건조단위중량의 경우 평균적으로 약 6%의 오차를 보였다. 이를 통해 개발한 Flat TDR 시스템의 정밀도를 확인할 수 있었다. Yu와 Jung이 사용한 오차보다 더 작은 오차를 보이므로 보다 더 정확한 값을 도출하는 것을 확인하였다.

(2) 본 연구에서는 모래를 통일분류법에 따라 나누어 비교 ‧ 분석하였으며, 함수비는 SP시료의 경우 약 0.7%, SM시료의 경우 약 1.3%의 오차를 보였다. 또한 건조단위중량은 SP시료의 경우 약 7%, SM시료의 경우 약 5%의 오차를 확인하였다. 실험 결과를 통하여 Flat TDR 시스템의 측정값이 기존의 전통적인 다짐관리방법과 유사한 값을 도출하는 것을 확인할 수 있었다. 이는 빠른 시공성과 경제성을 필요로 하는 건설현장에서 Flat TDR 장비가 적합하다는 것을 판단할 수 있었다.

(3) 본 연구를 통하여 개발한 Flat TDR 시스템의 현장적용을 위해서는 현장 시료를 채취하여 실내실험을 먼저 수행해야 하는 단점이 있지만, Flat TDR 시스템을 이용하여 흙의 함수비와 건조단위중량 측정하는 방법이 기존의 전통적인 다짐관리방법보다 신속하고 정확한 함수비와 건조단위중량을 도출할 수 있다. 본 연구는 추후 여러 가지 종류의 흙에 대하여 추가적인 연구를 통해 TDR 시스템의 정밀도와 신뢰도를 더욱 더 높이고 현장 적용의 실용화를 위한 기초 연구 자료로 활용할 수 있을 것으로 판단된다.

OPEN ACCESS

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.